
Współczesna nauka o sieciach wyrosła z teorii grafów. Dlatego też, choć fizycy upraszczają różne matematyczne pojęcia, warto rozpocząć wykład od paru matematycznych definicji.
Definicja 1. Sieć jest to zbiór wierzchołków połączonych krawędziami (możemy też powiedzieć: graf jest to zbiór węzłów i połączeń między nimi). Matematycznie graf o N wierzchołkach i E krawędziach oznaczamy symbolem G(N,E).
Definicja 2. Graf prosty G składa się z niepustego i skończonego zbioru V(G), którego elementy nazywamy wierzchołkami (lub węzłami) oraz skończonego zbioru E(G), którego elementami są różne nieuporządkowane pary różnych wierzchołków należących do zbioru V, tj. połączenia międzywęzłowe.
Wierzchołek reprezentuje zwykle pewien obiekt, a połączenie między wierzchołkami definiuje pewną relację między obiektami. Takim obiektem na przykład może być komputer, wtedy krawędź między wierzchołkami reprezentuje fizyczny przewód (na przykład światłowodowy), przez który dwa komputery położone na jego końcach komunikują się. Mówiąc prościej, schemat

mówi nam, że komputer A jest połączony z komputerem B. Ten sam schemat zastosowany do innych sytuacji może nam powiedzieć coś zupełnie innego, na przykład że osoba A zna osobę B albo że związek chemiczny A wchodzi w reakcję ze związkiem chemicznym B. Takich relacji może być naprawdę wiele:
| wierzchołek | połączenie | |
|---|---|---|
| społeczne | osoba |
znajomość kontakt seksualny wspólna publikacja naukowa połączenie telefoniczne ist e-mail |
| informacyjne | publikacja naukowa strona WWW klasa w programowaniu obiektowym |
cytowanie odnośnik (hyperlink) dziedziczenie |
| technologiczne | stacja transformatorowa lotnisko komputer |
przewód wysokiego napięcia połączenie lotnicze kabel (np. światłowodowy) |
| biologiczne | proteina gatunek neuron |
reakcja fizyczna pożywienie akson |
Definicja 2 opisuje najprostszy obiekt teorii grafów, graf prosty. Możemy ją uzupełnić na wiele sposobów. Jeśli na przykład wszystkim krawędziom grafu nadamy kierunki, uzyskamy graf skierowany (digraf). Ukierunkowana krawędź

będzie nam mówiła o tym, że wierzchołek A wpływa w pewien sposób na wierzchołek B. Na przykład publikacja A jest cytowana w publikacji B, na stronie internetowej A jest hiperłącze do strony internetowej B czy też osoba A jest przełożonym osoby B.
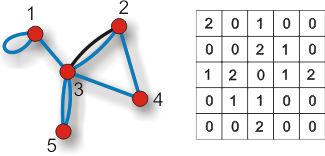
Z kolei multigraf to graf, w którym mogą występować krawędzie wielokrotne (gdy dwa wierzchołki są połączone więcej niż jedną krawędzią) oraz pętle (czyli krawędzie, których końcami jest ten sam wierzchołek).
Możemy też przypisać każdej krawędzi pewną wartość (wagę), reprezentującą na przykład przepustowość w sieci wodociągowej lub oporność w sieci elektrycznej. Otrzymamy w ten sposób graf z wagami, lub mówiąc prościej graf ważony.
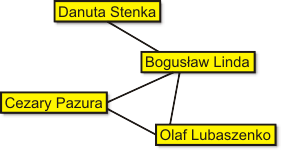
W końcu, możemy też analizować takie sieci, w których wierzchołki należą do dwóch rozłącznych zbiorów, a istniejące krawędzie łączą jedynie węzły z jednego zbioru z węzłami z drugiego zbioru (nigdy wewnątrz tego samego zbioru). Takie grafy nazywamy grafami dwudzielnymi. Przykładem jest sieć, w której do jednego zbioru należą aktorzy, zaś drugi zbiór stanowią filmy. Krawędź łączy obiekty należące do obu tych zbiorów wtedy, gdy aktor wystąpił w danym filmie. Fragment tak zdefiniowanej sieci aktorów wyglądałby na przykład tak:
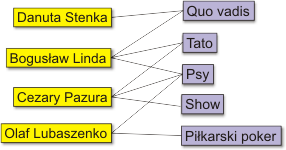
A tak wygląda rzutowanie (projekcja) grafu dwudzielnego na zbiór aktorów. W takiej projekcji krawędź łączy dwóch aktorów, jeśli wystąpili oni w tym samym filmie.
Podstawowym sposobem zobrazowania struktury grafu o rozmiarze N (oczywiście poza narysowaniem go) jest przedstawienie za pomocą macierzy kwadratowej N x N, zwanej macierzą sąsiedztwa A. Elementy aij tej macierzy są równe liczbie połączeń między węzłem i oraz j. W wypadku grafu prostego macierz jest symetryczna, a jej elementy są równe 0 (brak krawędzi) lub 1 (istnieje krawędź).
A oto przykład grafu skierowanego i jego macierzy sąsiedztwa::

W multigrafach elementy aij mogą być większe od jedności:
, a w grafach ważonych mogą być wyrażone dowolną liczbą rzeczywistą:
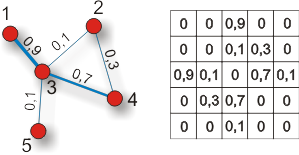
Elementy leżące na głównej przekątnej macierzy A są zwykle równe zeru chyba, że graf zawiera pętle. Spośród macierzy przedstawionych poniżej wybierz tę, która odpowiada prezentowanej sieci:
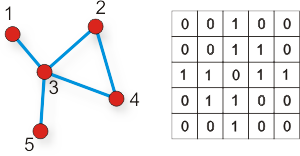
Podstawową charakterystyką węzła i jest jego stopień ki.
Definicja 3. Stopień ki wierzchołka (rząd, liczba koordynacyjna) jest to liczba bezpośrednich połączeń danego węzła z innymi wierzchołkami w sieci.
Wierzchołki połączone krawędzią nazywamy pierwszymi (najbliższymi) sąsiadami. Na przykład na rysunku poniżej
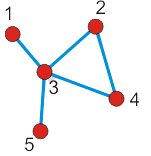
mamy odpowiednio k1 = 1, k2 = 2, k3 = 4, k4 = 2 i k5 = 1. Stopień węzła i w grafie prostym można wyrazić jako sumę elementów macierzy sąsiedztwa w kolumnie lub w wierszu i:
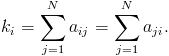
Znając stopnie wszystkich wierzchołków, możemy wyznaczyć liczbę wszystkich krawędzi w sieci:
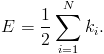
Możemy też obliczyć średni stopień wierzchołka:
![]()
W powyższym wzorze skorzystaliśmy z tzw. lematu o uściskach dłoni, który mówi, że suma stopni wszystkich węzłów w sieci jest równa podwojonej liczbie krawędzi (każda krawędź ma dwa końce, które dają przyczynek do tej sumy)
W wypadku sieci skierowanych musimy rozróżnić stopnie wejściowe kin węzła od stopni wyjściowych kout:
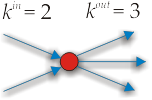
W sieciach skierowanych macierz sąsiedztwa nie jest symetryczna. Z tego powodu, suma elementów tej macierzy w i-tej kolumnie różni się od sumy elementów w i-tym wierszu. Sumując elementy macierzy sąsiedztwa wzdłuż kolumny, otrzymujemy stopień wejściowy węzła i, natomiast stopień wyjściowy otrzymujemy, sumując elementy aij wzdłuż i-tego wiersza tej macierzy:
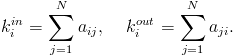
W wypadku sieci ważonych, w których każdej krawędzi jest przypisana waga, wprowadzono definicję stopnia ważonego, czyli siły węzła:
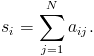
Definicja 4. Siłą węzła nazywamy sumę wag krawędzi przynależnych do tego węzła.
Definicja 5. Trasą w grafie G nazywamy ciąg wierzchołków i krawędzi postaci
![]() .
.
Zauważmy, że każdy wierzchołek w powyższej sekwencji sąsiaduje z wierzchołkiem, który go poprzedza jak również z wierzchołkiem, który następuje po nim.
Twierdzenie 1. Element (i,j) macierzy Ax jest równy liczbie różnych tras o długości x pomiędzy wierzchołkami i oraz j.
Dowód. Własność tę udowodnimy metodą indukcji matematycznej.
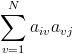 i
jest równa elementowi ij macierzy A2=A * A.
i
jest równa elementowi ij macierzy A2=A * A.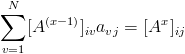 oznacza liczbę tras o
długości x pomiędzy i oraz j, co kończy dowód.
oznacza liczbę tras o
długości x pomiędzy i oraz j, co kończy dowód.
Definicja 6. Ścieżką nazywamy trasę, w której wszystkie krawędzie są
różne. Jeśli początek ścieżki pokrywa się z jej końcem i=j wtedy
mamy do czynienia z cyklem.
Definicja 7. Drogą w grafie G nazywamy ciąg krawędzi {{v1, v2}, {v2, v3}, ..., {vn-1, vn}}, taki, że koniec krawędzi {vi, vi+1} jest początkiem krawędzi {vi+1, vi+2} dla każdego i = 0, …, n-2 oraz taki, w którym wszystkie krawędzie i wszystkie wierzchołki są różne. Początek krawędzi {v1, v2} nazywamy początkiem drogi, a koniec krawędzi {vn-1, vn} końcem drogi. Długością drogi nazywamy liczbę tworzących ją krawędzi.
W grafie
przykładowymi drogami między wierzchołkami 2 i 5 są drogi {{2, 3}, {3, 5}} oraz {{2, 4}, {4, 3}, {3, 5}}. Pierwsza z nich ma długość 2, a druga 3. Pierwsza z rozpatrywanych dróg jest jednocześnie najkrótszą drogą między tymi wierzchołkami.
Definicja 6. Odległością d(i,j) wierzchołka i od wierzchołka j nazywamy długość najkrótszej drogi prowadzącej z i do j.
Mówiąc prostymi słowami, d(i, j) jest najmniejszą liczbą krawędzi, jakie należy przejść, by dostać się z wierzchołka i do wierzchołka j. O wierzchołkach odległych od siebie o x krawędzi mówimy, że są x-tymi sąsiadami.
Z definicji odległości międzywęzłowej d(i,j) oraz z twierdzenia 1 wynika, że jeśli graf G jest spójny, wtedy odległość pomiędzy dwoma dowolnymi wierzchołkami tego grafu i oraz j jest najmniejszą liczbą x, dla której pozycja (i,j) macierzy Ax jest różna od zera.
Definicja 7. Graf nazywamy spójnym, jeśli dla każdej pary wierzchołków istnieje droga je łącząca.
Prawie w każdej sieci rzeczywistej są węzły lub grupy węzłów niepołączone z resztą sieci. Na przykład w sieci komputerowej będą to komputery bez dostępu do Internetu, w sieci powiązań społecznych ludzie samotni, a w sieci dróg przykładem niespójności jest brak połączeń drogowych między różnymi kontynentami. Jeśli mamy do czynienia z taką sytuacją, mówimy, że graf jest niespójny, że składa się z pewnej liczby składowych spójnych (komponentów, klasterów). Doświadczenie mówi nam jednak, że w sieciach, które nas otaczają, zdecydowana większość węzłów należy do jednego wielkiego komponentu:

Podstawową strukturą w sieciach skierowanych jest największy słabo spójny komponent. Uzyskamy go, gdy zaniedbamy kierunki krawędzi i w powstałej w ten sposób sieci nieskierowanej znajdziemy największy spójny komponent. Wewnątrz niego możemy wyróżnić:
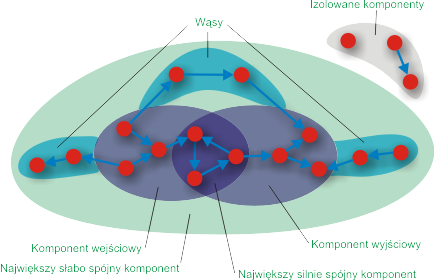
W obecnych czasach znajomość strukturalnej złożoności sieci skierowanych nabiera istotnego znaczenia w odniesieniu do sieci WWW. W tej sieci węzeł reprezentuje stronę internetową, a krawędź skierowana -- odnośnik (hyperlink) umieszczony na tej stronie, wskazujący na inną stronę. Oto fragment takiej sieci - sieć WWW Wydziału Fizyki Politechniki Warszawskiej. Lewa część rysunku przedstawia przykładową wędrówkę z wykorzystaniem odnośników po stronach wydziału. Z prawej strony pokazano graficzną reprezentację struktury całej sieci. Widoczne są w niej dwa silnie usieciowione, niemalże symetryczne klastery. Reprezentują one polską i angielską część serwisu informacyjnego wydziału. Zewnętrzne podsieci związane są z poszczególnymi zakładami naukowymi. Szczególnie rozbudowaną strukturę stron internetowych ma Zakład Fizyki Jądrowej (widoczną w górnej części rysunku).
W 2010 roku istnieje ponad 50 miliardów stron, zajmujących łącznie 1000 TB (terabajtów). Co miesiąc pojawia się 20 TB nowych stron. W 2000 roku naukowcy z firm IBM, Compaq i Altavista przeanalizowali ponad półtora miliarda połączeń między 200 milionami stron internetowych. Oszacowali oni, że jedynie 30% wszystkich stron znajduje się wewnątrz NSSK. Oznacza to, że większość przeszukiwarek internetowych indeksuje zaledwie jedną trzecią wszystkich stron. Dalsze 24% stron ma odnośniki umożliwiające dotarcie do rdzenia sieci. Kolejne 24% stron może być osiągnięte z NSSK. Pozostałe 22% stron reprezentuje zamknięte grupy wewnątrz przedsiębiorstw, całkowicie odizolowane od rdzenia Internetu. Choć od czasu przeprowadzenia tych badań Internet poważnie się rozwinął i powyższe liczby mogą się znacząco różnić od tych, jakie znaleźlibyśmy, badając strukturę Internetu dzisiaj, dają jednak pewne wyobrażenie o wielkościach omówionych wcześniej struktur w jednej z najpopularniejszych sieci skierowanych.
Idea spójności ma wiele wspólnego z fizyczną teorią perkolacji. Póki co, udowodnimy ciekawe twierdzenie dotyczące zagadnienia spójności w grafach prostych.
Twierdzenie 2. Niech graf G będzie grafem prostym mającym N wierzchołków. Jeśli graf G ma t składowych, to liczba E jego krawędzi spełnia nierówności
![]()
Dowód. Prawdziwość dolnego ograniczenia ![]() udowodnimy przez indukcję względem liczby krawędzi grafu G. Dla
grafu pustego(grafem pustym nazywamy graf, w którym
zbiór krawędzi jest zbiorem pustym.) ta nierówność jest trywialna.
Jeśli graf G ma najmniejszą możliwą liczbę krawędzi
udowodnimy przez indukcję względem liczby krawędzi grafu G. Dla
grafu pustego(grafem pustym nazywamy graf, w którym
zbiór krawędzi jest zbiorem pustym.) ta nierówność jest trywialna.
Jeśli graf G ma najmniejszą możliwą liczbę krawędzi
![]() , to usunięcie którejkolwiek krawędzi powoduje zwiększenie liczby składowych o 1 i powstały w ten sposób graf
ma N wierzchołków, t+1 składowych oraz
, to usunięcie którejkolwiek krawędzi powoduje zwiększenie liczby składowych o 1 i powstały w ten sposób graf
ma N wierzchołków, t+1 składowych oraz ![]() krawędzi. Z założenia indukcyjnego wynika,
że
krawędzi. Z założenia indukcyjnego wynika,
że ![]() , skąd otrzymujemy
, skąd otrzymujemy
![]() , czego należało dowieść.
, czego należało dowieść.
Aby dowieść ograniczenia górnego załóżmy, że każda składowa grafu
G jest grafem pełnym (grafem pełnym nazywamy graf
prosty, w którym każdy wierzchołek ma połączenie z każdym innym
wierzchołkiem w sieci. Graf pełny o N wierzchołkach posiada
![]() krawędzi.). Przypuśćmy, zatem, że istnieją dwie
składowe G1 oraz G2 mające odpowiednio N1 i N2
wierzchołków, przy czym niech
krawędzi.). Przypuśćmy, zatem, że istnieją dwie
składowe G1 oraz G2 mające odpowiednio N1 i N2
wierzchołków, przy czym niech ![]() . Zauważmy,
że jeśli zastąpimy składowe G1 oraz G2 dwoma innymi grafami
pełnymi mającymi odpowiednio N1+1 oraz N2-1
wierzchołków, to całkowita liczba wierzchołków nie zmieni się, a
całkowita liczba krawędzi zmieni się o wielkość:
. Zauważmy,
że jeśli zastąpimy składowe G1 oraz G2 dwoma innymi grafami
pełnymi mającymi odpowiednio N1+1 oraz N2-1
wierzchołków, to całkowita liczba wierzchołków nie zmieni się, a
całkowita liczba krawędzi zmieni się o wielkość: ![]() ,
która jest liczbą dodatnią. Wynika stąd, że aby graf G miał
maksymalną liczbę krawędzi, musi składać się z grafu pełnego
mającego N-t+1) wierzchołków i z (t-1) wierzchołków
izolowanych. Stąd wynika teza twierdzenia.
,
która jest liczbą dodatnią. Wynika stąd, że aby graf G miał
maksymalną liczbę krawędzi, musi składać się z grafu pełnego
mającego N-t+1) wierzchołków i z (t-1) wierzchołków
izolowanych. Stąd wynika teza twierdzenia.
Uwaga. Powyższe twierdzenie nie jest prawdziwe w drugą stronę tzn. jeśli liczba krawędzi grafu spełnia nierówności z twierdzenia, nie oznacza to, że graf jest spójny.
Definicja 8. Lasem nazywamy graf prosty nie zawierający cykli, a drzewem las spójny.
Przykładem drzewa może być drzewo (!), układ krwionośny w nerce, lub dorzecze Amazonki.

A to właśnie jest las. Składa się on z pięciu składowych, z których każda jest drzewem.

Poniższe twierdzenie podaje kilka prostych własności drzew.
Twierdzenie 3.Niech T będzie grafem mającym N wierzchołków. Wtedy następujące warunki są równoważne:
Dowód. Dla N=1 twierdzenie jest trywialne. Załóżmy zatem, że
N >1 . Dowiedźmy, że z warunku 1 wynika 2, ![]() .
.
Własność tę dowiedziemy metodą indukcji matematycznej. Przypadek N =2 jest trywialny. Dla N >2 zauważamy, że ponieważ T jest drzewem i z definicji nie zawiera cykli, więc usunięcie którejkolwiek krawędzi musi spowodować rozpad T na dwa grafy, z których każdy jest drzewem o rozmiarach odpowiednio N1 i N2, przy czym N1+ N2=N. Z założenia indukcyjnego wynika, że liczba krawędzi w każdym z tych nowych drzew wynosi odpowiednio N1-1 oraz N2-1. Wynika stąd, że liczba krawędzi w grafie wyjściowym jest równa (N1-1)+(N2-1)+1=N-1, co kończy dowód.
![]() Własność tę udowodnimy przez sprzeczność.
Załóżmy, że graf T jest niespójny i składa się z t > 1
składowych. Liczba krawędzi w tym grafie jest równa sumie krawędzi
we wszystkich jego składowych. Ponieważ graf nie ma cykli zatem z
poprzedniej własności wynika, że liczba krawędzi w każdej
składowej jest o jeden mniejsza od liczby wierzchołków w tej
składowej. Wynika stąd, że suma krawędzi w całym grafie wynosi:
Własność tę udowodnimy przez sprzeczność.
Załóżmy, że graf T jest niespójny i składa się z t > 1
składowych. Liczba krawędzi w tym grafie jest równa sumie krawędzi
we wszystkich jego składowych. Ponieważ graf nie ma cykli zatem z
poprzedniej własności wynika, że liczba krawędzi w każdej
składowej jest o jeden mniejsza od liczby wierzchołków w tej
składowej. Wynika stąd, że suma krawędzi w całym grafie wynosi:
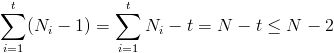 dla t > 1, co przeczy założeniu, że liczba krawędzi w tym grafie
wynosi N -1.
dla t > 1, co przeczy założeniu, że liczba krawędzi w tym grafie
wynosi N -1.
![]() . Usunięcie którejkolwiek krawędzi powoduje
powstanie grafu mającego N wierzchołków i N-2 krawędzi. Z
Twierdzenia 2 wynika, że taki graf musi być niespójny.
. Usunięcie którejkolwiek krawędzi powoduje
powstanie grafu mającego N wierzchołków i N-2 krawędzi. Z
Twierdzenia 2 wynika, że taki graf musi być niespójny.
![]() . Ponieważ graf T jest spójny, każda para
wierzchołków jest połączona co najmniej jedną drogą. Jeśli daną
parę wierzchołków łączą dwie drogi, to zataczają one pewien cykl,
co przeczy temu, że drzewo nie zawiera cykli.
. Ponieważ graf T jest spójny, każda para
wierzchołków jest połączona co najmniej jedną drogą. Jeśli daną
parę wierzchołków łączą dwie drogi, to zataczają one pewien cykl,
co przeczy temu, że drzewo nie zawiera cykli.
![]() . Jeśli do drzewa T dodamy dowolną krawędź
{i, j} , wtedy utworzymy cykl, ponieważ po dodaniu tej krawędzi
istnieją dwie drogi pomiędzy wierzchołkami i oraz j. To, że
zostanie utworzony dokładnie jeden cykl jest konsekwencją innej
własności grafów, że jeśli dwa różne cylke w grafie zawierają tę
samą krawędź e, to w tym grafie istnieje cykl nie zawierający
tej krawędzi. Gdyby dodanie nowej krawędzi {i, j} spowodowało
utworzenie kilku cykli, wtedy na mocy przytoczonej własności
musiałyby istnieć co najmiej trzy drogi pomiędzy wierzchołkami i oraz j.
. Jeśli do drzewa T dodamy dowolną krawędź
{i, j} , wtedy utworzymy cykl, ponieważ po dodaniu tej krawędzi
istnieją dwie drogi pomiędzy wierzchołkami i oraz j. To, że
zostanie utworzony dokładnie jeden cykl jest konsekwencją innej
własności grafów, że jeśli dwa różne cylke w grafie zawierają tę
samą krawędź e, to w tym grafie istnieje cykl nie zawierający
tej krawędzi. Gdyby dodanie nowej krawędzi {i, j} spowodowało
utworzenie kilku cykli, wtedy na mocy przytoczonej własności
musiałyby istnieć co najmiej trzy drogi pomiędzy wierzchołkami i oraz j.
Powyższe własności powodują, że obliczenia analityczne na drzewach są znacznie prostsze niż na grafach z cyklami. Jeśli chcemy dowieść jakiegoś twierdzenia na grafach, to często wygodnie jest dowieść go najpierw dla drzew. Co więcej, wiele hipotez, których nie udowodniono jeszcze dla dowolnych grafów, dowiedziono dla drzew. Teoria sieci złożonych zaniedbując cykle (wszystkie lub tylko krótkie) i przybliżając badane sieci strukturami drzewiastymi często korzysta z własności drzew.
Z punktu widzenia fizyki statystycznej sieci jednym z najciekawszych twierdzeń dotyczących drzew jest podane niżej twierdzenie Cayley'a.
Twierdzenie 4 . (Cayley, 1889) Istnieje N(N-2) różnych drzew mających N wierzchołków.
Dowód tego twierdzenia można znaleźć w książce Robina J. Wilsona pt. Wprowadzenie do teorii grafów, PWN Warszawa 1998.}
Z tego twierdzenia wynika, że podanie liczby wierzchołków drzewa
nie precyzuje z jakim drzewem mamy do czynienia.
Podobnie jest w przypadku grafów nie będących drzewami - istnieje
wiele różnych mikroskopowych realizacji grafów o zadanej
liczbie wierzchołków i krawędzi. Jeśli chcemy sprecyzować, którą
realizację mamy na myśli musimy się posłużyć macierzą sąsiedztwa
zawierającą kompletną informację o strukturze badanego grafu.
Badanie macierzy sąsiedztwa nie jest jednak łatwe, a w przypadku
dużych grafów prawie niewykonalne. W takich przypadkach korzystne
jest zdefiniowanie i posługiwanie się parametrami uśrednionymi po
wszystkich możliwych realizacjach tego grafu. Postępowanie to jest
odpowiednikiem znanego z fizyki statystycznej uśredniania po
przestrzeni fazowej. Mikrostan Ω grafu jest w pełni
charakteryzowany przez macierz sąsiedztwa Ω ≡ A, zaś
odpowiednikiem przestrzeni fazowej stanowiącej zbiór wszystkich
możliwych mikrostanów jest Γ ≡ {A}. W przypadku drzew
o zadanym rozmiarze N objętość przestrzeni fazowej wynosi
oczywiście ![]() .
.
Rozważając pewną wielkość makroskopową X zdefiniowaną na
grafie (np. średnią odległość między węzłami) musimy pamiętać, że
jest ona funkcją mikrostanu grafu X ≡ X(A). Później, w dalszej części wykładu
zdefiniujemy kilka użytecznych makroskopowych
parametrów grafu. Omawiając te parametry dla wprowadzonych
modeli sieciowych, będziemy się
już posługiwali uśrednionymi po całej przestrzeni fazowej
wartościami ![]() ,
gdzie
,
gdzie ![]() oznacza liczbę wszystkich możliwych
mikrostanów modelu.
oznacza liczbę wszystkich możliwych
mikrostanów modelu.
Spójrzmy, na poniższe trzy drzewa:
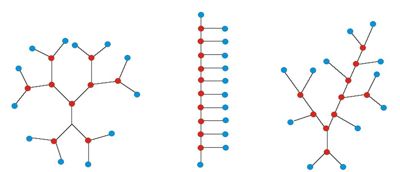
Zwróćmy uwagę, że chociaż niektóre z makroskopowych
parametrów tych drzew, np. średni stopień wierzchołka <k> = 21/11 i rozmiar drzewa N = 22, są identyczne,
to mikroskopowa struktura każdego z drzew jest inna. Z Twierdzenia
Cayley'a wynika, że liczba różnych mikroskopowych realizacji drzew
o rozmiarze N = 22 wynosi 2220.