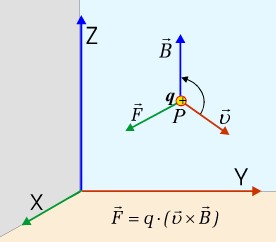
Siła Lorentza

Z faktu, że ruch ładunków elektrycznych powoduje powstawanie pola magnetycznego zaś ładunki będące w spoczynku pola magnetycznego nie wytwarzają  wynika, że pole magnetyczne powinno oddziaływać na poruszające się w nim ładunki elektryczne, nie powinno zaś działać na ładunki będące w spoczynku. Zostało to rzeczywiście stwierdzone doświadczalnie. 

Rys.10.2.1. Siła Lorentza	Na ładunki poruszające się w polu magnetycznym działa tzw. siła Lorentza, która określona jest przez wektor indukcji magnetycznej ,  wartość ładunku  i prędkość z jaką ładunek ten porusza się w polu magnetycznym - następującym wzorem
		(10.2.1)
	Widzimy, że siła działająca na ładunek poruszający się w polu magnetycznym jest zawsze prostopadła zarówno do kierunku wektora jego prędkości, jak i do kierunku wektora indukcji magnetycznej. Zwrot tej siły zależny jest od znaku poruszającego się ładunku.

Zależność ta umożliwia ilościowe zdefiniowanie wektora indukcji magnetycznej:

Jeżeli na ładunek poruszający się z prędkością działa w punkcie siła określona wzorem (10.2.1) to w punkcie tym istnieje pole magnetyczne o  indukcji , określonej tym wzorem przez siłę, ładunek i prędkość.

Wartość siły Lorentza zależy zgodnie z własnością iloczynu wektorowego od kąta między wektorem prędkości ładunku i wektorem indukcji magnetycznej

Jeśli cząstka naładowana porusza się prostopadle do kierunku wektora , to siła ta ma maksymalną wartość równą

Możemy więc powiedzieć, że  wartość indukcji magnetycznej jest  równa sile jaka działa na jednostkowy ładunek dodatni (próbny) poruszający się w polu magnetycznym z jednostkową prędkością w kierunku, w którym siła magnetyczna ma maksymalną wartość.

Siła elektrodynamiczna

Na razie jednak rozważać będziemy tylko pole magnetyczne, które na każdy poruszający się ładunek działa siłą określoną wzorem (10.2.1). Jak wiemy, uporządkowany ruch ładunków w przewodniku nazywamy prądem elektrycznym. Prąd ten charakteryzujemy natężeniem prądu I, które określone jest wzorem (9.1.1) Wykorzystajmy to dla zapisania siły Lorentza działającej na ładunek poruszający się z prędkością w przewodniku znajdującym się w polu magnetycznym o indukcji

Wektor prędkości zapisaliśmy jako stosunek przemieszczenia ładunku wzdłuż osi przewodnika do czasu, w którym to przemieszczenie nastąpiło. Otrzymaliśmy w ten sposób wyrażenie określające siłę działająca na element przewodnika przez który płynie prąd o natężeniu I.  Siłę tę nazywamy siłą elektrodynamiczną (lub siłą Ampera). Pamiętając o własnościach  iloczynu wektorowego widzimy, że kiedy przewodnik ustawiony jest wzdłuż kierunku pola to nie działa na niego żadna siła, kiedy ustawiony jest prostopadle do kierunku pola - siła jest największa. Wartość tej siły jest proporcjonalna do natężenia prądu w przewodniku.

Oddziaływanie wzajemne przewodników z prądem

Wykorzystajmy prawo Ampera oraz wzór na siłę Lorentza do wyznaczenia siły oddziaływania wzajemnego dwóch nieskończenie długich przewodników. 

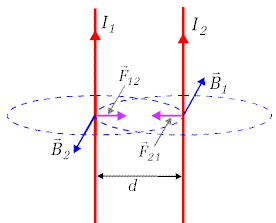Przyjmijmy, że w przewodnikach płyną prądy I1 oraz I2 , a ich wzajemna odległość wynosi d.  Na Rys. 10.2.2. kolorem czerwonym pokazane są przewodniki, kolorem niebieskim zaznaczone są okręgi wokół nich oraz wektory indukcji magnetycznej od przewodnika pierwszego w miejscu gdzie znajduje się drugi  i vice versa. Kolorem fioletowym zaznaczone są kierunki sił wzajemnie na siebie działających przewodników. Widać, że kiedy prądy I1 oraz I2  skierowane są w tę samą stronę, to przewodniki będą się przyciągać, kiedy w strony przeciwne, będą się odpychać.

Rys.10.2.2. Siła oddziaływania dwóch nieskończonych przewodników z prądem

Wykorzystując wzory (10.2.3) oraz (10.1.4) i pamiętając, że kąt pomiędzy osią przewodnika i wektorem indukcji jest kątem prostym otrzymujemy skalarny wzór na wartość siły działającej na odcinek o długości  l  (np. l₁) danego przewodnika ( np. tego z prądem I₁₎  pochodzący od pola magnetycznego wytworzonego przez drugi przewodnik (z prądem I₂₎,

Symetryczne wyrażenie możemy napisać dla drugiej siły. Wykonując obustronne dzielenie przez  element długości przewodnika uzyskujemy wyrażenie określające siłę działającą na jednostkę jego długości. 

Opuściliśmy tu indeksy dolne, bowiem zauważamy, że wartości sił działających na jednostkę długości każdego z przewodników określone są tym samym wyrażeniem. Tak zdefiniowana siła wyrażona jest w  N/m.

Oddziaływanie na siebie dwóch przewodników jest podstawą definicji jednostki natężenia prądu elektrycznego - ampera (1A), którą podajemy poniżej.

 Jeden amper (1A) to natężenie takiego stałego  prądu elektrycznego, który płynąc w dwóch równoległych, nieskończenie długich przewodach o znikomo małym okrągłym przekroju, znajdujących się w próżni w odległości wzajemnej 1m powoduje powstawanie między nimi siły równej na każdy metr ich długości. 

Z tej definicji ampera wynika też wartość przenikalności magnetycznej próżni