Rozchodzenie się światła, podobnie jak i fal elektromagnetycznych o innych długościach, polega na przemieszczaniu się w czasie i przestrzeni drgań wektorów natężeń pól: elektrycznego i magnetycznego. Prędkość światła w próżni oznaczyliśmy symbolem c. W innych ośrodkach prędkość ta, jak wynika z równań Maxwella, jest mniejsza i zależy od względnej przenikalności elektrycznej i magnetycznej ośrodka,

Współczynnik załamania ośrodka  definiujemy wzorem 

a więc prędkość światła w danym ośrodku można wyrazić następująco:

Na początek kilka uwag. 

1. Przybliżona równość we wzorze (10.1.1b)  wynika z faktu, że dla większości ośrodków, w których rozważamy rozchodzenie się światła, wartość przenikalności magnetycznej jest na tyle bliska jedności, że można ją tu pominąć. Otrzymujemy w ten sposób wynikającą z równań Maxwella interesującą zależność między współczynnikiem załamania i przenikalnością elektryczną dla większości (nie ferromagnetycznych) ośrodków, . Dodajmy do tego jeszcze, że chociaż w falach elektromagnetycznych mamy do czynienia z drganiami wektorów i , to doświadczalnie stwierdzono decydującą role drgań pola elektrycznego dla reakcji fotochemicznych, fotoelektrycznych czy również fizjologicznych. Dlatego w rozważaniach naszych będziemy mówić o drganiach wektora natężenia pola elektrycznego jako o drganiach wektora świetlnego.
2. Pod pojęciem natężenia lub intensywności fali świetlnej będziemy tu rozumieć wielkość proporcjonalną nie do amplitudy drgań wektora , a do kwadratu tej amplitudy, bowiem,  jak pamiętamy, energia fali elektromagnetycznej jest proporcjonalna do kwadratu natężenia pola elektrycznego, wzór (9.6.1a). Pod sformułowaniem "amplituda fali" będziemy więc rozumieli, amplitudę drgań elektrycznych zaś w celu wyznaczenia intensywności lub "natężenia światła" będziemy wyznaczać wielkość proporcjonalną do kwadratu amplitudy. 
3. Stosunek prędkości światła w próżni do prędkości światła w danym ośrodku oznaczyliśmy symbolem n i nazywamy współczynnikiem załamania. W niektórych przypadkach będziemy też używać symbolu n dla oznaczania rzędu widma interferencyjnego, bądź dyfrakcyjnego, ale z kontekstu będzie wynikało jasno o jaką wielkość chodzi.  
4. Omawiając zjawiska falowe będziemy odnosić je do fal świetlnych, ale pamiętajmy, że omawiane tu zjawiska i stosowany przez nas opis dotyczą także innych długości fal.

Wszystkie omawiane w tej lekcji zjawiska mogą być opisane z użyciem formalizmu równań Maxwella. Zjawiska te i prawidłowości nimi rządzące zostały jednak zaobserwowane znacznie wcześniej. Zostały one opisane w ramach fenomenologicznych zasad,  które umożliwiały w prosty sposób zrozumienie zjawisk falowych nie rozpatrując elektromagnetycznej natury samych fal, z czego nie zdawano sobie wcześniej sprawy. Dopiero Maxwell pokazał, że światło ma naturę fal elektromagnetycznych.

Prosty opis wielu zjawisk falowych umożliwia zasada podana przez Christiana Huyghensa w 1678 roku, a więc prawie dwa wieki przed sformułowaniem przez Maxwella równań fal elektromagnetycznych. Zasada ta nie zakłada elektromagnetycznego charakteru fal świetlnych i nie wymaga znajomości prędkości ich rozchodzenia się.  Mimo to jest niezwykle użyteczna do opisu wielu zjawisk obserwowanych w optyce. Warto dodać, że zasada ta ma charakter ogólny i może być stosowana do opisu różnego rodzaju fal.

Zasadę Huyghensa można sformułować następująco.

Każdy punkt w przestrzeni, do którego dociera fala, staje się źródłem nowej fali kulistej. 

Zasada ta umożliwia wyjaśnienie wielu zjawisk optycznych i będziemy powoływać się na nią wiele razy w tej lekcji. Na początek zastosujmy tę zasadę do opisu zjawiska załamania światła na granicy dwóch ośrodków.

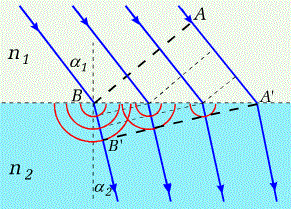Niech czoło fali rozchodzącej się w prędkością w pierwszym ośrodku o współczynniku załamania n1 , pada na granicę z drugim ośrodkiem o współczynniku załamania n2 i rozchodzi się dalej w z prędkością . Zgodnie z zasadą Huyghensa, w ośrodku tym rozchodzą się fale kuliste, które na rysunku pokazane są kolorem czerwonym. W czasie, kiedy światło przebiegnie w ośrodku pierwszym odcinek AA', fala w ośrodku drugim przebiegnie odcinek BB'.  Pamiętamy przy tym, że współczynnik załamania wiąże się z prędkością fali związkiem .

Rys.10.1.2. Zasada Hyughensa dla załamania światła na granicy dwóch ośrodków

.Zgodnie z oznaczeniami na rysunku 10.1.2 mamy więc zależności

 z czego natychmiast wynika, że

Jest to znane ze szkoły prawo Snelliusa.

Druga zasada, sformułowana przez Pierre'a Fermata w 1650 roku dotyczy czasu przejścia światła pomiędzy dwoma punktami. Jej sens można sformułować następująco.

Światło biegnie po takiej drodze, na pokonanie której potrzebny jest ekstremalny (na ogół najmniejszy) czas.

Zasada ta umożliwia na przykład sformułowanie praw odbicia i załamania fal poprzez znalezienie warunków minimalnego czasu na pokonanie drogi pomiędzy dwoma zadanymi punktami.

Sformułujmy te prawa posługując się zasadą Fermata.

Rys.10.1.3. Zasada Fermata dla odbicia fal	Rys.10.1.4. Zasada Fermata dla załamania fal

Warunki geometryczne dla odbicia promieni świetlnych od granicy dwóch ośrodków pokazane są na rysunku 10.1.3. "Próbny" promień pokazany jest kolorem czerwonym. Ośrodek jest wciąż ten sam, więc światło porusza się cały czas z tą samą prędkością. Minimum czasu odpowiada więc  najkrótszej drodze. Długość drogi pomiędzy punktami A i B ,określonej tak, że promień świetlny musi w jakimś punkcie odbić się od zwierciadła Z, może być zapisana w postaci

 Poszukujemy takiej wartości x, dla której droga l  mieć będzie wartość minimalną. W tym celu obliczamy pochodną dl/dx  i przyrównujemy ją do zera. Otrzymujemy

co można też zapisać w postaci

 a z tego wynika natychmiast znane ze szkoły prawo, że kąt padania równy jest kątowi odbicia. Światło pobiegnie więc od punktu A do punktu B po takiej drodze, by spełniony był warunek (10.1.6), a wiec nie po drodze APB, ale AP'B.

Podobnie możemy otrzymać  prawo załamania promieni świetlnych na granicy dwóch ośrodków o współczynnikach załamania n₁ i n₂. Relacje geometryczne przedstawia rysunek 10.1.4. Pamiętając, że współczynnik załamania jest stosunkiem prędkości światła w próżni do prędkości w danym ośrodku, tj. otrzymujemy wyrażenie na czas przebycia przez światło drogi od A do B 

.

(10.1.7)

 Wielkość l nosi nazwę drogi optycznej. Poszukujemy więc takiej wartości x, przy ustalonych położeniach punktów A i B (patrz rysunek 10.1.4), by droga ta była minimalna. W tym celu obliczamy pochodną wyrażenia, w którym drogę optyczną określamy w funkcji x,

co, podobnie jak w przykładzie z odbiciem światła, przedstawiamy w postaci

a stąd wynika natychmiast prawo załamania

Światło pobiegnie więc po drodze, dłuższej niż prosty odcinek łączący punkty A i B . (linia przerywana koloru czerwonego na rysunku 10.1.4). Zasada Fermata mówi jednak, ze to nie droga ma być najkrótsza, ale czas przebycia drogi, a to odpowiada najkrótszej drodze optycznej. Zauważmy, że z zasady Fermata możemy też określić czy kąt załamania będzie mniejszy, czy większy od kąta padania. Zależy to od relacji pomiędzy współczynnikami załamania obu ośrodków.

Warto tu dodać, że zasada Fermata jest szczególnym przypadkiem tzw. zasady wariacyjnej, według której dla rozwiązania danego zagadnienia poszukuje się takiej funkcji, dla której określona całka przyjmuje wartość ekstremalną. W naszych przykładach całką tą była sumaryczna droga  lub sumaryczny czas. Zasada ta umożliwia rozwiązywanie wielu problemów nie tylko z dziedziny fizyki.