W roku 1900 Max Planck zaproponował inny opis widma promieniowania ciała doskonale czarnego. Przyjął on zupełnie rewolucyjną jak na owe czasy hipotezę, że emitowane promieniowanie ma nieciągły rozkład, że emitowane jest pewnymi porcjami, czyli jest skwantowane. Procesy zachodzące we wnęce stanowiącej ciało doskonale czarne rozważał on jako drgania oscylatorów harmonicznych, które emitują i absorbują promieniowanie. Energie tych oscylatorów, według założenia Plancka,  nie mogą przyjmować jednak  dowolnych wartości, ale tylko takie, dla których spełniony jest warunek

(11.2.1)

 gdzie n jest liczbą naturalną, h jest stałą, która później została nazwana stałą Plancka; jest częstotliwością drgań oscylatora. Z zależności tej widać, że najmniejsze energie emitowanego przez taki oscylator promieniowania odpowiadają zmianie liczby n o jeden, czyli  

(11.2.2)

Dla wyznaczenia średniej energii oscylatorów Planck przyjął, że ich rozkład opisany jest znanym z termodynamiki rozkładem Boltzmanna; Patrz: kurs Fizyka I, wzór (12.35a). 

(11.2.3)

gdzie jest liczbą oscylatorów mających energię ,   jest  współczynnikiem normalizacyjnym, k jest stałą Boltzmanna i T jest temperaturą wyrażoną w kelwinach. Sumaryczna energia tych oscylatorów jest iloczynem ich liczby przez energię jednego z nich , czyli

(11.2.4)

Średnia energia oscylatora określona jest jako suma energii wszystkich oscylatorów podzielona przez sumaryczną ich liczbę czyli

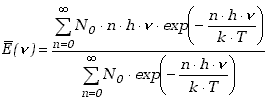(11.2.5)

Wykonując pomocniczą zamianę zmiennych i sumowanie nieskończonych szeregów, które okazują się zbieżne, otrzymuje się wyrażenie na średnią energię oscylatora. (Szczegóły tych obliczeń można znaleźć np. w pozycji 3, podanej bibliografii.) W rezultacie otrzymujemy

(11.2.6)

Średnia energia oscylatora jest tu funkcją częstotliwości. Właśnie na tym polega zasadnicza różnica pomiędzy obliczeniami Plancka i  Rayleigha-Jeansa, gdzie średnia energia nie zależała od częstotliwości i była równa kT. Zauważmy, że kiedy częstotliwości są bardzo małe, to wyrażenie można zastąpić przez początkowe wyrazy rozwinięcia w szereg potęgowy tj. , a wstawiając to do wzoru (11.2.6) otrzymujemy na średnią energię wyrażenie , jak we wzorze Rayleigha-Jeansa. Kiedy jednak , to jak widać z postaci tego wzoru,  średnia energia zmierza do zera (mianownik zmierza do nieskończoności, więc ułamek zmierza do zera). 

Dla wyznaczenia gęstości energii promieniowania Planck pomnożył tę średnią wartość przez czynnik wyrażający prawdopodobieństwo występowania danej częstotliwości w widmie promieniowania, analogicznie jak we wzorze Rayleigha-Jeansa,  otrzymując wyrażenie

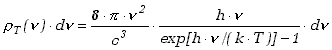(11.2.7)

Jest to wzór Plancka określający gęstość energii promieniowania ciała doskonale czarnego. Wzór ten doskonale zgadza się z danymi doświadczalnymi w całym obszarze widmowym. Podkreślamy jeszcze raz, że cała różnica pomiędzy tym  wzorem, a wzorem Rayleigha-Jeansa (11.1.4) polega na zamianie stałej wartości średniej energii promieniowania na wartość zależną od częstotliwości. Ta zależność pojawiła się jako konsekwencja założenia, sprzecznego z fizyką klasyczną, że energia wypromieniowywana jest skokowo w postaci kwantów, a nie w sposób ciągły.

Wzór Plancka często wyrażany jest w funkcji długości fali, a nie częstotliwości. Pamiętając, że wielkości te związane są zależnością, widzimy, że wzrost częstotliwości powoduje zmniejszenie długości fali tzn. . Ujemny znak wyraża tu odwrotny kierunek zmiany jednej wielkości względem zmiany drugiej. Wyraża to także znak pochodnej . Mamy więc

(11.2.8)

 Po podstawieniu we wzorze (11.2.7) i uwzględnieniu związku (11.2.8) otrzymujemy

(11.2.9)

Stała odgrywająca kluczową role we wzorze Plancka może być otrzymana jako parametr przy dopasowaniu wzoru (11.2.7) do danych doświadczalnych. Wartość tej stałej wyznaczona została także z innych zależności, które poznamy w dalszej części naszego kursu. Wartość stałej Plancka wynosi

(11.2.10)

Często używa się stałej , oznaczonej symbolem i nazywanej "h kreślone". Wartość tej stałej równa jest

(11.2.11)

Liczby w nawiasach oznaczają niedokładność ostatnich cyfr znaczących.

Początkowo Planck zastosował swoją hipotezę do opisu promieniowania ciała doskonale czarnego. Później rozszerzył ja na wszelkie zjawiska fizyczne w postaci postulatu stwierdzającego, że kwantowanie dotyczy wszelkich obiektów fizycznych o jednym stopniu swobody, których stan zmienia się jak sinusoidalna funkcja czasu, czyli wykonuje proste drgania harmoniczne. Energia całkowita takiego obiektu może przyjmować tylko wartości będące wielokrotnością stałej Plancka, czyli

(11.2.12)

To, że w makroskopowych zjawiskach, np. ruchu wahadła,  nie zauważamy ich kwantowego charakteru wynika z bardzo małej wartości stałej Plancka. Wiele przykładów zjawisk w skali mikroświata, gdzie kwantowanie jest widoczne,  poznamy w dalszej części naszego kursu.

Dzień 14 grudnia 1900 roku, kiedy to max Planck przedstawił swoją teorię promieniowania ciała doskonale czarnego wprowadzając koncepcję kwantu na posiedzeniu Niemieckiego Towarzystwa Fizycznego w Berlinie, został uznany za dzień narodzin mechaniki kwantowej.