Jeśli są to ładunki o takich samych wartościach ale różnych znakach: oraz odległość między nimi jest dużo mniejsza niż odległość do punktu , w których wyznaczmy pole, to układ taki nazywamy dipolem elektrycznym; Układ taki pokazany jest na rysunku 2.4.1., gdzie jednak nie są zachowane proporcje dotyczące odległości punktu . Prostą przechodzącą przez oba ładunki nazywamy osią dipola (na rysunku oś ta pokrywa się z osią X); wektor łączący oba ładunki  i skierowany w kierunku ładunku dodatniego nazywamy ramieniem dipola (na rysunku zaznaczony kolorem niebieskim), zaś iloczyn ramienia dipola przez wartość ładunku dodatniego nazywamy elektrycznym momentem dipolowym, .Wektor ten zaznaczony jest na rysunku kolorem różowym (2.4.1) Warto zaznaczyć, że elektryczne własności molekuł dielektryków podobne są do własności dipoli.

Rys. 2.4.1. Dipol elektryczny

Natężenie pola w danym punkcie przestrzeni pochodzące od dipola możemy wyznaczyć korzystając z zasady superpozycji pól tj. sumując natężenia pól pochodzących od obu ładunków. 

Rozpatrzmy dwie najprostsze sytuacje. 

W przypadku gdy rozważany punkt znajduje się na osi dipola, to wektor natężenia pola leży również na tej osi. Ilustruje to rysunek 2.4.2

Wektory natężeń pól od ładunku dodatniego i ujemnego leżą na tej samej osi ale są przeciwnie skierowane. Natężenie pola jest więc ich różnicą arytmetyczną;  patrz rysunek 2.4.2.

gdzie przez oznaczyliśmy odległość punktu od środka dipola. Pamiętając o założeniu, że odległość ta jest znacznie większa od odległości pomiędzy ładunkami, tj. , otrzymujemy

 Drugim szczególnym przypadkiem jest położenie punktu na prostej prostopadłej do osi dipola i przechodzącej przez jego środek. Przypadek ten ilustruje Rys. 2.4.3.  

	Wartości bezwzględne natężeń pól pochodzących od obu ładunków są takie same i wynoszą (2.4.5)  Z relacji geometrycznych pokazanych na rysunku 2.4.3 widzimy że  (2.4.6) oraz, że (2.4.7)
Rys.2.4.3. Pole elektryczne dipola na prostej przechodzącej przez jego środek i prostopadłej do jego osi

Podstawiając do wzoru (2.4.6) wartości natężeń ze wzoru (2.4.5) oraz ze wzoru (2.4.7) otrzymujemy

Pamiętając znów, że i zaniedbując wielkość w porównaniu z  otrzymujemy

Porównując wzory (2.4.4) i (2.4.9) widzimy, że natężenie pola w punktach jednakowo odległych od środka dipola jest dwukrotnie większe dla  punktów leżących na jego osi w stosunku do punktów leżących na prostej prostopadłej do osi dipola i przechodzącej przez jego środek. Zauważmy również, że pole elektryczne pochodzące od dipola zmniejsza się proporcjonalnie do tj. szybciej niż pole pochodzące od ładunku punktowego, które zmniejsza się jak .  Nic dziwnego, sumaryczny ładunek dipola wynosi zero.

Dla kompletności podamy jeszcze bez wyprowadzania wzór na pole dipola w dowolnym punkcie, którego położenie określa odległość  i kąt 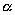 , zgodnie z rysunkiem 2.4.1. 

Dla kąta 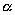równego 0 i 90 stopni wzór ten przechodzi odpowiednio we wzory (2.4.4) i (2.4.9).

Dla ilustracji, na rysunku 2.4.4 pokazane są linie sił pola dla dipola elektrycznego oraz prostopadłe do nich linie odpowiadające przecięciu powierzchni ekwipotencjalnych z płaszczyzną XY. Dla kilku punktów pokazane są też wektory natężenia pola, które zawsze są styczne do linii sił pola. 

Spróbuj także sam określić kierunek i oszacować wartość natężenia pola w innych punktach. 

	Na dipol umieszczony w jednorodnym polu elektrycznym działa para sił, której moment wynosi (patrz rysunek 2.4.4) (2.4.11) co w postaci wektorowej można zapisać jako (2.4.12) Moment sił będzie więc powodował obrót dipola tak, by jego oś ustawiona była wzdłuż linii sił pola elektrycznego . Wtedy i wektor momentu dipolowego będzie równoległy do wektora .
Rys.2.4.5. Dipol w polu elektrycznym

 Obrót dipola w polu elektrycznym wymaga wykonania pewnej pracy. Praca ta może być wyrażona jako iloczyn momentu pary sił działających na dipol i kąta jego obrotu. Moment ten dla jednorodnego pola elektrycznego zależy od wartości kąta zgodnie ze wzorem (2.4.11). Pracę musimy zapisać więc jako całkę uwzględniającą tę zależność. Jako kąt początkowy weźmy ustawienie poprzeczne dipola . Obrót wykonujemy więc od tej wartości do wartości kąta równej .

(Kąt po którym wykonujemy całkowanie oznaczyliśmy (jedynie dla rozróżnienia) jako ) Praca ta jest miarą energii potencjalnej dipola w jednorodnym polu elektrycznym. Zapiszemy to w postaci

 gdzie skorzystaliśmy z własności iloczynu skalarnego. Energia potencjalna dipola w polu elektrycznym wyrażona jest wiec poprzez iloczyn skalarny wektorów: momentu dipolowego i natężenia pola elektrycznego.