![]() .
.
Przypomnijmy jeszcze raz wzór (4.2.1) określający siłę Lorentza, czyli siłę działającą na ładunek poruszający się w polu magnetycznym,
|
|
(5.4.1) |
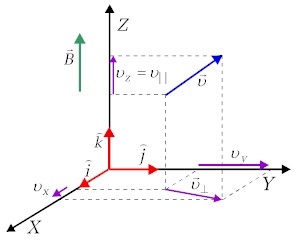 |
Zapiszmy składowe tego wektora. Ustawmy układ współrzędnych
prostokątnych tak, by oś Z pokrywała się z
kierunkiem wektora indukcji magnetycznej |
| Rys 5.4.1. Wektor indukcji i składowe wektora prędkości w układzie współrzędnych prostokątnych. |
Zapiszemy składowe siły ![]() przedstawiając
iloczyn wektorowy we wzorze (5.4.1) w postaci wyznacznika:
przedstawiając
iloczyn wektorowy we wzorze (5.4.1) w postaci wyznacznika:
|
|
(5.4.2) |
Zwróćmy uwagę, że siła w kierunku równoległym do kierunku wektora
indukcji magnetycznej wynosi zero, zaś siły w kierunkach prostopadłych są
wprost proporcjonalne do wartości wektora ![]() ,
przy czym siła w kierunku X jest proporcjonalna do składowej prędkości
w kierunku Y , a siła w kierunku Y do składowej prędkości
w kierunku X.
,
przy czym siła w kierunku X jest proporcjonalna do składowej prędkości
w kierunku Y , a siła w kierunku Y do składowej prędkości
w kierunku X.
Kiedy cząstka spoczywa lub porusza się równolegle do kierunku pola magnetycznego, to nie działa na nią żadna siła pomimo, że znajduje się w polu magnetycznym. Jest to zasadnicza różnica w porównaniu z działaniem na cząstki naładowane pola elektrycznego.
Równania ruchu mają postać
|
. |
(5.4.3) |
W równaniach z prawej strony wprowadziliśmy oznaczenie:
|
|
(5.4.4) |
Wielkość ![]() odgrywa zasadnicza rolę w zagadnieniu ruchu cząstki naładowanej w polu
magnetycznym i nosi nazwę częstości cyklotronowej.
Zwróćmy uwagę, że wielkość ta pozostaje stała w czasie ruchu jeśli tylko
pozostają stałe: q, B i m.
odgrywa zasadnicza rolę w zagadnieniu ruchu cząstki naładowanej w polu
magnetycznym i nosi nazwę częstości cyklotronowej.
Zwróćmy uwagę, że wielkość ta pozostaje stała w czasie ruchu jeśli tylko
pozostają stałe: q, B i m.
(UWAGA: Teraz zmieniamy kolor czcionki. Znaczy to, że jeśli bardzo nie lubisz rozszyfrowywać formuł matematycznych, to możesz fragment pisany tym kolorem opuścić, ale stracisz wtedy ciągłość naszych rozważań.)
Zapiszmy warunki początkowe, czyli położenie i prędkość cząstki dla t=0
|
|
(5.4.5) |
Równania ruchu możemy teraz zapisać w postaci
|
|
(5.4.6) |
Skorzystaliśmy tu z faktu, że kiedy pochodna funkcji równa jest zeru, to funkcja równa jest stałej, a za wartości stałych podstawiliśmy wartości prędkości dla t=0.
Z pierwszego z równań po prawej stronie wzoru (5.4.6) możemy wyznaczyć y, a następnie pochodną dy/dt,
|
|
|
(5.4.7) |
Wstawiając wyrażenie na pochodną dy/dt do drugiego z równań po prawej stronie wzoru (5.4.6) otrzymujemy
|
|
co możemy też zapisać w postaci |
|
(5.4.8) |
Pamiętając, że wyrażenie ![]() zachowuje wartość stałą w czasie możemy równanie po prawej stronie wzoru
(5.4.8) przepisać w postaci
zachowuje wartość stałą w czasie możemy równanie po prawej stronie wzoru
(5.4.8) przepisać w postaci
|
|
(5.4.9) |
Równanie powyższe stanowi końcowy wynik pierwszego etapu naszych rozważań. Równanie to jest analogiczne do równania oscylatora harmonicznego, które znamy z kursu Fizyka I, i którego postać i rozwiązanie przytaczamy poniżej
|
równanie oscylatora harmonicznego: |
rozwiązanie równania oscylatora harmonicznego: |
|
|
|
|
(5.4.10) |
gdzie ![]() oraz
oraz ![]() są stałymi, które można wyznaczyć z warunków początkowych.
są stałymi, które można wyznaczyć z warunków początkowych.
Rozwiązanie równania (5.4.6) ma więc postać
|
|
(5.4.11) |
Pochodna względem czasu, czyli prędkość wzdłuż osi X wynosi
|
|
(5.4.12) |
Wstawiając to wyrażenie do pierwszego z równań po prawej stronie wzoru (5.4.6) otrzymujemy postać rozwiązania równania ruchu dla składowej y. Rozwiązanie dla składowej z, to po prostu równanie ruchu jednostajnie prostoliniowego, co wynika bezpośrednio z postaci trzeciego z równań (5.4.6). Ostatecznie, rozwiązanie równań ruchu cząstki w polu magnetycznym w układzie współrzędnych prostokątnych ma postać.
|
|
(5.4.13) |
Stałe dowolne ![]() oraz
oraz ![]() wyznaczamy, jak zwykle, z warunków początkowych. Dla współrzędnej x
mamy na podstawie wzorów (5.4.13) i (5.4.5) dla t=0:
wyznaczamy, jak zwykle, z warunków początkowych. Dla współrzędnej x
mamy na podstawie wzorów (5.4.13) i (5.4.5) dla t=0:
|
|
(5.4.14) |
Dzieląc stronami równanie (b) przez równanie (a) we wzorze (5.4.14) otrzymujemy
|
|
(5.4.15) |
Widzimy, że faza naszego ruchu harmonicznego, określona jest przez kierunek początkowy rzutu wektora prędkości początkowej na płaszczyznę prostopadłą do kierunku wektora indukcji pola magnetycznego.
Dla wyznaczenia stałej A przekształcimy równanie (a) we wzorze (5.4.14)
|
|
(5.4.16) |
gdzie skorzystaliśmy z trygonometrycznej równości ![]() .
.
Ostatecznie otrzymujemy równana ruchu cząstki naładowanej w polu magnetycznym, dla warunków początkowych określonych wzorem (5.4.5). Są to równania ruchu harmonicznego we współrzędnych X i Y (co odpowiada równaniu okręgu w płaszczyźnie XY) oraz równanie prostej we współrzędnej Z.
|
|
(5.4.17) |
Dla znalezienia równania toru podnosimy do kwadratu i dodajemy stronami równania ruchu dla współrzędnych x i y.
|
|
(5.4.18) |
Otrzymaliśmy znane z matematyki równanie okręgu.
Tor cząstki w płaszczyźnie prostopadłej do pola jest okręgiem
którego środek znajduje się w punkcie określonym przez współrzędne ![]() oraz
oraz
![]() i o promieniu równym
i o promieniu równym ![]() .
Wartości te określone są wzorami:
.
Wartości te określone są wzorami:
|
|
(5.4.19) |
gdzie iloczyn ![]() jest tzw. "składową poprzeczną" pędu cząstki.
jest tzw. "składową poprzeczną" pędu cząstki.
W kierunku osi Z tor jest linią prostą, zaś w płaszczyźnie XY okręgiem. Wobec tego wypadkowy tor będzie linią śrubową zwaną też helisą.. Parametry tej krzywej (skok linii śrubowej i jej promień) nie zależą od czasu. Stąd bardzo ważny wniosek: pole magnetyczne zmienia jedynie kierunek wektora prędkości, nie zmienia jednak jego wartości bezwzględnej.
Opisane zależności możesz teraz sam sprawdzić korzystając z ilustracji interaktywnej demonstrującej ruch cząstki naładowanej w polu magnetycznym dla zadanych przez Ciebie wartości parametrów. Odpowiedz na zawarte tam pytania
| MS-Excel | Interaktywna ilustracja graficzna |
Kliknij w polu rysunku. |
| Rys.5.4.2. Przykład ruchu cząstki w polu magnetycznym. | ||