Własności pola magnetycznego

Poprowadźmy dalej rozumowanie rozpoczęte we wstępie. Umieśćmy igłę magnetyczną w płaszczyźnie prostopadłej do kierunku przewodnika z prądem i zbadajmy dokładniej kierunek jej ustawienia się w wytworzonym przez poruszające się ładunki polu, Rys. 10.1.1.

Rezultat był do przewidzenia. Liniowy kształt przewodnika narzuca symetrię osiową całego układu. Kierunek ustawienia się igły w różnych punktach pokazują na rysunku niebieskie linie przerywane. Linie te stanowią analogię linii sił pola elektrycznego i nazywane są liniami indukcji pola magnetycznego.
Zauważamy tu istotną różnicę pomiędzy kierunkami sił działających na igłę magnetyczną a kierunkami linii sił pola elektrycznego, które skierowane były do lub od ładunków elektrycznych zaczynając lub kończąc się na nich. Linie indukcji magnetycznej nie mają początku ani końca, ale są zamknięte i otaczają przewodnik z prądem.

Rys.10.1.1. Pole magnetyczne przewodnika z prądem

Wektor indukcji magnetycznej

Do ilościowego opisu własności pola magnetycznego wprowadzono wektor zwany wektorem indukcji magnetycznej,. Wektor ten charakteryzuje pole magnetyczne podobnie jak wektor , czyli wektor natężenia pola elektrycznego, charakteryzuje pole elektryczne. Kierunek tego wektora pokrywa się z kierunkiem linii indukcji wzdłuż których ustawia się igła magnetyczna. Podobnie jak dla wektora , dla wektora obowiązuje także zasada superpozycji według której pole wytwarzane przez wiele poruszających się swobodnych ładunków lub prądów elektrycznych w przewodnikach równe jest wektorowej sumie pól wytwarzanych przez każdy poruszający się ładunek i prąd traktowany oddzielnie. Zapisujemy to w postaci

(10.1.1)

gdzie sumowanie rozciąga się na wszystkie poruszające się ładunki i prądy.

Prawo Ampère'a

Obliczmy całkę wektora indukcji magnetycznej po konturze zamkniętym . Dla prostoliniowego przewodnika nie będzie to trudne, bo linie indukcji są współśrodkowymi okręgami. Wektor indukcji będzie więc zawsze styczny do odpowiadającemu mu okręgu, zaś wartość całki będzie proporcjonalna do natężenia prądu płynącego w przewodniku.

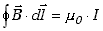(10.1.2)

Zapisaliśmy tę zależność w postaci wektorowej słusznej też dla przypadków, kiedy kontur nie jest okręgiem współśrodkowym. Współczynnik proporcjonalności 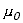zwany jest przenikalnością magnetyczną próżni. Równanie (10.1.2) nosi nazwę prawa Ampère'a. Oczywiście, całka w tym równaniu ma wartość zero, jeśli w przewodniku obejmowanym przez dany kontur prąd nie płynie lub kiedy kontur nie obejmuje przewodnika.

Prawo Ampère'a umożliwia łatwe wyznaczenie wartości wektora indukcji magnetycznej w zadanej odległości od nieskończenie długiego przewodnika, w którym płynie prąd o natężeniu I. W tym celu obliczamy całkę po okręgu o promieniu r współśrodkowym z przewodnikiem. Otrzymamy

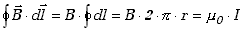(10.1.3)

Skorzystaliśmy tu z faktu, że wektory 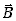i 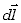są w tym przypadku zawsze do siebie równoległe, bo linie wektora indukcji są okręgami współśrodkowymi z przewodnikiem tak samo jak kontur po którym wykonujemy całkowanie.

Wartość wektora indukcji w odległości r od przewodnika wynosi więc

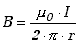(10.1.4)

Wektor ten jest styczny w danym punkcie do okręgu, po którym wykonane zostało całkowanie.

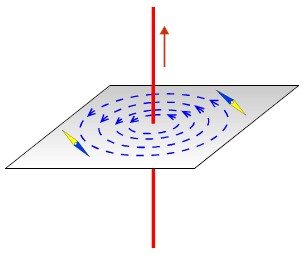
Pole magnetyczne solenoidu

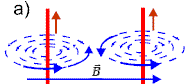
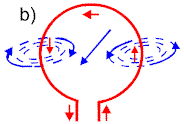
Ważnym zastosowaniem prawa Ampère'a jest wyznaczenie pola magnetycznego wewnątrz solenoidu, który stanowi wiele zwojów przewodnika nawiniętych jeden obok drugiego i w takiej liczbie, że jego długość jest znacznie większa od średnicy. Na rysunku 10.1.2.a) pokazane są elementy dwóch sąsiednich zwojów oddalone od siebie, by zademonstrować konfigurację pola magnetycznego wokół nich. Rysunek 10.1.2.b) pokazuje pole jednego zwoju solenoidu.


Rys.10.1.2. Pole: a) fragmentu dwóch sąsiednich zwojów, b) jednego zwoju solenoidu

Widzimy, że pola pomiędzy sąsiednimi zwojami kompensują się, natomiast pola od strony wewnętrznej i na zewnątrz solenoidu dodają się. Pole wewnątrz i na zewnątrz jest symetryczne względem osi solenoidu. Kierunek wektora indukcji magnetycznej pokrywa się z kierunkiem tej osi.

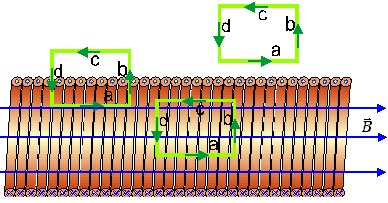
Rys 10.1.3. Pole magnetyczne solenoidu; strzałki niebieskie pokazują kierunek pola magnetycznego; ramki i strzałki zielone - obwody po których liczymy cyrkulację

Rysunek 10.1.3. przedstawia w przekroju fragment solenoidu który będziemy traktować jako nieskończenie długi. Dla wyznaczenia wartości wektora indukcji skorzystamy z prawa Ampere'a obliczając całkę z wektora 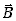wzdłuż zamkniętego konturu zgodnie ze wzorem (10.1.2). Dla uproszczenia naszych rozważań nadamy konturowi postać prostokątnej ramki, której boki a i c ułożone są równolegle do osi solenoidu, a boki b i d są do tej osi prostopadłe. Zauważamy natychmiast, że całka ta liczona zarówno dla ramki znajdującej się całkowicie wewnątrz solenoidu jak i dla tej na zewnątrz równa jest zeru, bowiem w obu przypadkach ramki nie obejmują przewodników z prądem. (Co nie znaczy bynajmniej, że nie ma tam pola magnetycznego.) Zauważany też, że wkład do całki od boków b i d jest we wszystkich przypadkach równy zeru, bowiem wektor 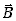jest prostopadły do tych boków i iloczyn skalarny we wzorze (10.1.2) równy jest zeru. Wynika z tego bardzo ważny wniosek. Wkłady od boków a i c kompensują się wewnątrz i na zewnątrz solenoidu co oznacza, że panuje tam jednorodne pola magnetyczne.

Wniosek ten zawiera faktycznie dwa stwierdzenia. Pierwsze, że pole magnetyczne w całej przestrzeni wewnątrz solenoidu jest jednorodne, czyli takie samo co do wartości i kierunku. Drugie, że pole w całej przestrzeni zewnętrznej też jest jednorodne. Brzmi to paradoksalnie, bowiem przestrzeń ta rozciąga się do nieskończoności. Oczekiwalibyśmy raczej, że pole zmniejsza się ze wzrostem odległości od solenoidu. Co więcej - pamiętamy, że linie wektora indukcji magnetycznej są zamknięte i ten sam skończony strumień przenika przez ograniczoną powierzchnię przekroju poprzecznego wewnątrz solenoidu, co i przez nieskończoną powierzchnię wokół solenoidu na zewnątrz. Oba te warunki mogą być spełnione równocześnie tylko wtedy, kiedy pole magnetyczne na zewnątrz solenoidu równe jest zeru.

Pamiętajmy jednak, że rozważamy tu solenoid o nieskończonej długości. W rzeczywistych solenoidach o długościach skończonych występują też składowe pola wzdłuż boków b i d. Pole na zewnątrz rzeczywistego solenoidu nie jest więc dokładnie równe zeru, choć znacznie mniejsze niż wewnątrz. Wartość tego pola zależna od położenia punktu względem osi i środka solenoidu.

Powróćmy do wyznaczenia wartości indukcji magnetycznej wewnątrz solenoidu o nieskończonej długości. W tym celu umieśćmy ramkę tak by jej bok a znajdował się wewnątrz solenoidu, a bok c na zewnątrz. Wiemy już teraz, że niezerowy wkład wnosi wyłącznie bok a.

Przyjmijmy, że na jednostkę długości solenoidu przypada n zwojów. W takim przypadku wzór (10.1.2) sprowadza się do całkowania wzdłuż tego tylko boku w rezultacie czego otrzymujemy wzór na wartość wektora indukcji magnetycznej wewnątrz solenoidu

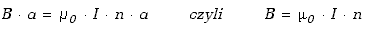(10.1.5)

Pole magnetyczne wewnątrz solenoidu proporcjonalne jest do natężenia prądu i gęstości zwojów solenoidu. Ten prosty wzór obowiązuje ściśle dla solenoidu o nieskończonej długości. W praktyce, przybliża on nieźle wartość indukcji pola magnetycznego punktach znajdujących się w środkowej części solenoidów o długościach skończonych.

Solenoidy jako urządzenia służące do wytwarzania pola magnetycznego znajdują zastosowanie w wielu różnorodnych instrumentach pomiarowych oraz w eksperymentach fizycznych. O skali wielkości stosowanych solenoidów świadczy zamieszczona obok fotografia.
Fot.10.1.1. Jeden z etapów konstrukcji detektora STAR w Brookhaven National Laboratory (USA). "STAR" - to pierwsze litery słów "Solenoidal Tracker At RHIC" - co można przetłumaczyć jako "Solenoidalny tropiciel w RHIC" i służy do "tropienia" cząstek elementarnych. Tej średnicy solenoid służy do wytwarzania pola magnetycznego w eksperymencie STAR. Więcej o samym laboratorium powiemy w dalszej części.

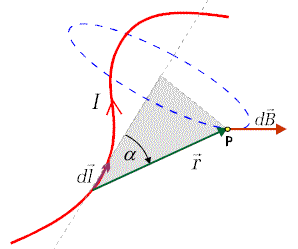
Prawo Biota-Savarta

Zwykle jednak mamy do czynienia z bardziej złożonym rozkładem prądów elektrycznych. Wyznaczenie wektora indukcji magnetycznej w dowolnym punkcie umożliwia w takim przypadku prawo Biota-Savarta.

Rozważmy krzywoliniowy przewodnik, w którym płynie prąd o natężeniu I, Rys.10.1.2. Przewodnik ten możemy rozłożyć na sumę bardzo dużej liczby elementów z których każdy możemy uznać za prostoliniowy. Elementowi takiemu przypisujemy wektor jego długości

skierowany zgodnie z kierunkiem przepływu przezeń prądu. Interesuje nas wektor indukcji pola magnetycznego w punkcie P, którego położenie wyznacza promień wodzący

określony względem danego elementu przewodnika.

Rys.10.1.2. Prawo Biota-Savarta

Zgodnie z prawem Biota-Savarta indukcję pola magnetycznego w tym punkcie pochodzącą od elementu 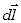określa wzór

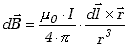(10.1.6

W formie skalarnej prawo Biota-Savarta możemy zapisać w postaci

,
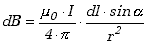(10.1.7)

gdzie kąt 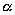zawarty jest pomiędzy elementem 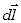i promieniem 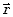. Ważnym wnioskiem z prawa Biota-Savarta jest to, że pole magnetyczne od przewodnika o dowolnym kształcie, jest wprost proporcjonalne do natężenia prądu płynącego w tym przewodniku .

Dla wyznaczenia wypadkowego wektora indukcji magnetycznej pochodzącego od całego przewodnika należy obliczyć całkę z wyrażenia (10.1.6) po całkowitej długości przewodnika.

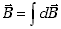(10.1.8)

Prawo Gaussa

Zapiszmy definicję strumienia wektora indukcji magnetycznej przez dowolną powierzchnię S .

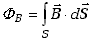(10.1.9)

Podobnie, jak dla wektora natężenia pola elektrycznego, zapiszmy teraz prawo Gaussa dla wektora indukcji magnetycznej. Zwróćmy tu jednak uwagę na zasadniczą różnicę pomiędzy własnościami pola elektrycznego i magnetycznego. W przypadku natężenia pola elektrycznego, linie sił zaczynały i kończyły się na ładunkach elektrycznych. Linie indukcji magnetycznej nie mają początku ani końca. Obliczając więc strumień wektora indukcji magnetycznej przez dowolną zamkniętą powierzchnię otrzymamy zawsze tyle linii wchodzących co i wychodzących.

Prawo Gaussa dla pola magnetycznego oznacza, że nie ma ładunków magnetycznych mogących stanowić początek lub koniec linii sił wektora 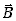i zawsze

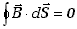(10.1.9a)

Oznacza to, że w przyrodzie nie istnieją pojedyncze bieguny magnetyczne.